1. Background

Amongst the Woodger papers in the Wroughton Archives is a flowchart (below) for NIM on Pilot Ace. Called NIM 2, there is no date and no author's name. The code pre-dates November 1951 because it uses TS8 and TS9 instead of DL's 8 and 9. It possibly dates to before Pilot Ace was built and there is no evidence a version ever ran on Pilot Ace.

NIM is a game in which two players take turns in removing objects from discrete piles. Each player in turn must remove at least one object, and may remove more than one of the objects, but all the objects must be from the same pile. Sometimes the goal is to be the last player to take an object; sometimes (misère game) it is to force your opponent to take the last object.

The game is thought to be very old. Its current name was coined by Charles Bouton who developed the theory of the game in 1901. The theory uses the binary "exclusive or", written here as ⊕, to calculate "nim-sums". The winning strategy is to ensure that the nim-sum of the piles is zero when you complete your move. This is always possible if the nim-sum is not zero before your move.

For example, faced with three piles (A, B, C) of 3, 4 and 5 objects, your first step would be:

• find the nim-sum of the piles:
  S = 3 ⊕ 4 ⊕ 5 = {011} ⊕ {100} ⊕ {101} = {010} = 2
• check each heap
  A: 3 ⊕ S = {011} ⊕ {010} = {001} = 1
  B: 4 ⊕ S = {100} ⊕ {010} = {110} = 6
  C: 5 ⊕ S = {101} ⊕ {010} = {111} = 7
• the only pile that is reduced is A. Remove 2 objects from A.

The full game might proceed as follows:

• A  B C nim-sum
•  3  4  5   {010}   you take 2 from A, leaving nim-sum equal to zero.
•  1  4  5   {000}   opponent takes 2 from C
•  1  4  3   {010}   you take 2 from B
•  1  2  3   {000}   opponent takes 1 from C
•  1  2  2   {001}   you take 1 from A
•  0  2  2   {000}   opponent takes 1 from C
•  0  2  1   {011}   in normal play, following the "rules" to ensure you take the last object; you would take 1 object from B leaving two piles.
  To force your opponent to take the last object you have to depart from the rules in the end game, and in this case you would take the
  whole of pile B.

Wikipedia has a substantial article about NIM.

2. NIM 3

NIM 2 had the limited objective of finding a winning move for a given set of piles or advising that no such move was available. Playing with physical piles outside the computer, the operator would have to adjust for the recommended move or deal with the losing situation, observe his opponent's move, then feed the new pile sizes into the computer for more advice.

I think it is clear that NIM 2 was not meant to be a demonstration program - few lay persons are familiar with binary numbers and hardly anybody with the backwards binary it uses.

In fact the Pilot Ace has ample capacity to play a full game against an operator, as witness NIM 3. I wrote this version of NIM in 2016, based on NIM 2. Program cards suitable to play the game on the emulator can be downloaded here and a flow chart of the program is shown at the end of this page.

The object of NIM 3 is to be the last player to take a piece. Some notes:

• the maximum number of objects in a pile is 31
• the maximum number of piles is 6.

To play the game:

• Load program nim3.crd and press Initial Input. Program stops on {1 0-25 s}.
• Indicate the number n (1 ≤ n ≤ 31) of objects in the first pile with a 1 in P_n (bit n) of the ID and press Single Shot.
• Repeat this operation for the remaining piles.
• If six piles are input the program automatically proceeds to the game phase. If there are 5 piles or less, end the input process by setting P₃₂ of the ID to 1 and pressing Single Shot.
• Program stops on {3 3-3 } showing the contents of the piles on the OS
• single shot to {1 0-25 }, then select P₃₂=1 for the computer to have the first move, or zero for the operator to have the first move.
• If it is the computer's turn it will
  • stops on {2 15-16 } showing the size of the pile it will modify. Single shot.
  • stops on {6 4-4 } showing the amended size of that pile. Single shot.
  • stops on {6 14-14 } showing the updated status of the piles. It is now the operator's turn
• Operator's turn
  • clear the OS and press Single Shot.
  • nominate the pile you wish to modify by entering it's size in the ID
  • nominate how many objects to remove, in the ID
  • stops on {3 6-6 } showing the new pile sizes on the OS
  • single shot returns control to the computer

Example: in the case mentioned above where there are three piles (A, B, C) containing 3, 4 and 5 objects and the operator wants the computer to move first, the game would progress as follows (ss is single shot, i.e. press the "ONE SHOT" switch once):

• Load program nim3.crd and press Initial Input. Then:

  stop          action
• {1 0-25  s} clear ID (press the "CLEAR ID" switch); ss
• {1 0-25    } set P₅=1 on ID; ss (to input pile size of 5)
• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₄=1 on ID; ss (to input pile size of 4)
• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₃=1 on ID; ss (to input pile size of 3)
• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₃₂=1 on ID; ss (to terminate input)
• {1 0-25  s} clear ID; ss
• {3 3-3    s} clear OS (press the "CLEAR OPS" switch); ss (OS shows the current sizes of the piles. The piles are in P_2-6, P_7-11, P_12-16 and the current pile sizes are 3, 4, 5. Note that the values are expressed in backwards binary - least significant bit on the left)

• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₃₂=1 on ID; ss (instruct the computer to take first turn)
• {2 15-16  } OS = 3; clear OS; ss (shows contents of the pile the computer will adjust)
• {6 4-4      } OS = 1; clear OS; ss (shows adjusted contents of that pile)
• {6 14-14  } clear OS; ss (1, 4, 5 are the new pile sizes; now operator's turn).

• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₅=1 on ID; ss (selecting pile of size 5)
• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₂=1 on ID; ss (remove 2 objects)
• {3 6-6    s} clear OS; ss (1, 4, 3 are the new pile sizes, now computer's turn)

• {2 15-16  } OS = 3; clear OS; ss (shows contents of pile the computer will adjust)
• {6 4-4      } OS = 1; clear OS; ss (shows adjusted contents of that pile)
• {6 14-14  } clear OS; ss (1, 2, 3 are the new pile sizes; now operator's turn).

• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₅=1 on ID; ss (select pile of size 5)
• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₂=1 on ID; ss (remove 2 objects)
• {3 6-6    s} clear OS; ss (1, 2, 2 are the new pile sizes)

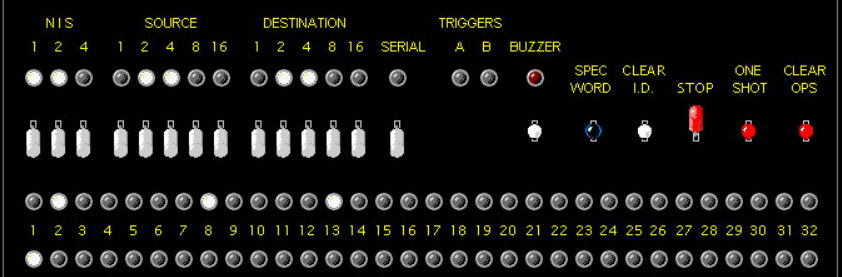
• {2 15-16  } OS = 1; clear OS; ss (shows contents of pile it will adjust)
• {6 4-4      } OS = 0; clear OS; ss (shows adjusted contents of that pile)
• {6 14-14  } clear OS; ss (0, 2, 2 are the new pile sizes; now operator's turn).

• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₂=1 on ID; ss (selecting pile of size 2)
• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₁=1 on ID; ss (remove 1 objects)
• {3 6-6    s} clear OS; ss (0, 1, 2 are the new pile sizes)

• {2 15-16  } OS = 2; clear OS; ss (OS shows contents of pile it will adjust)
• {6 4-4      } OS = 1; clear OS; ss (shows adjusted contents of that pile)
• {6 14-14  } clear OS; ss (0, 1, 1 are the new pile sizes; now operator's turn).

• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₁=1 on ID; ss (selecting pile of size 1)
• {1 0-25  s} clear ID; ss
• {1 0-25    } set P₁=1 on ID; ss (remove 1 objects)
• {3 6-6    s} clear OS; ss (0, 0, 1 are the new pile sizes)

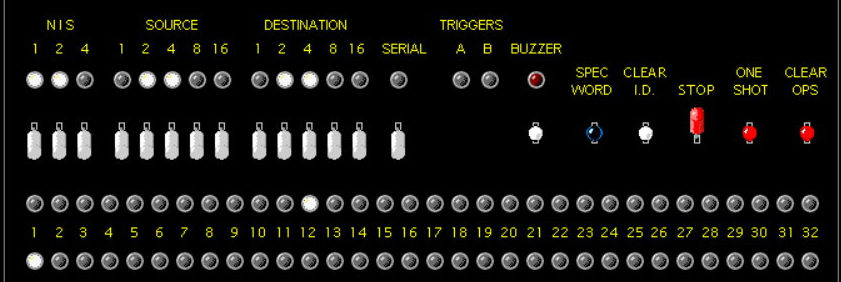
• {2 15-16  } OS = 1; clear OS; ss (OS shows contents of pile computer will adjust)
• {6 4-4      } OS = 0; clear OS; ss (shows adjusted contents of that pile)
• {3 15-15  } (computer wins)

• ss for new game

3. Flow Chart of NIM 3

©2010-2024 David Richard Green. All rights reserved.
dgreen@uraone.com