

The instrument [1] described below is primarily intended to quickly and accurately evaluate the curves drawn by recording devices. It avoids the need for averaging or other calculations, because when "optically tracing" a curve, a thermogram, barogram, etc., the planimeter guided over the recording strip indicates the mean height (ordinate) directly, without the need to also trace along the Ordinate and abscissa axes (zero line).
As is well known, recording strips can be evaluated with all precision planimeters by tracing around the curve together with the axes as a surface, calculating the content and dividing it by the abscissa, most appropriately with the roller planimeter, which is expensive and whose tracing arm must be set to the abscissa length each time to avoid calculation as much as possible. However, as the optical planimeter can be used to easily measure strongly wave-shaped curves up to 30 or 40 cm long in one or two minutes with an average error of less than 0.1 mm, its performance exceeds that of expensive devices. It also has other more or less valuable properties, such as: various types of area calculations, the automatic drawing of the mean integral curve, hyperbolas, etc. and the possibility of perspective measurement of large areas (leather measuring machine). However, since other, sometimes more suitable instruments are already commercially available for these purposes, less emphasis has been placed on this in the following description.
The 20 to 25 cm long apparatus [2] shown in two different versions in Fig. l consists, similar to Prytz's rod planimeter, of a rod or frame aa with thread f, index i, the sharp-edged wheel (or cutting edge) r and a partially perforated, double plane mirror s attached above or next to the wheel on a bridge, which is vertical when in use, but can be folded down onto the frame for packing. To solve drawing tasks, the bridge has a draw spring. The handling differs from other planimeters because there is no tracing pin. This is replaced by the "optical tracing point" that still needs to be defined in more detail.
For use, the instrument is placed on a paper base p (Fig. 2 and 3), which is designed as follows [3]. You measure the distance of the wheel axis from the index i (equal to Ri) and mark the point R at this distance from the edge of the paper with a small circle, draw the line l which can have any curves at the ends, parallel to the edge at twice the distance and draw a perpendicular from R on l, which is extended. A less important bifurcated curve intersecting the extension is designed based on a simple formula given in the second section.
This system is placed on the registration strip (Fig. 2) in such a way that the edge lays along the ordinate of the starting point U of the curve k to be evaluated and the latter falls into the extension of the perpendicular to l. The instrument must now be placed on the system with the wheel in R so that the thread is in the extension of the plumb line and the index i on the planimeter falls on U. If you look from any point B into the broken plane mirror t, the image of the intersection of f and l appears in U, which may be called the "optical tracing point". At the beginning of the process you use the lower part of the mirror and only later the upper part in order to clearly see the index and the curve through the fine interruptions in the silver coating. Even when viewing obliquely, the observer notices two images of the intersection of f and l, which belong to a moving and a fixed ray. The optical tracing point is the image that is further away from the observer and instrument and is associated with the fixed beam, which is also characterized by its clarity in front of the moving image. During navigation, the apparatus and recording strips must be well lit and the thread must not be shaded by the mirror. If the mirror is vertical, the optical tracing point does not change its position when you alternately look at the top and bottom of the mirror surface. However, every movement of the planimeter caused by the guide c (see also Fig. 1) changes the position of this point, and it is
It is very easy to guide the instrument in such a way that it tracks along the curve k from U to the end point U1 with the same certainty as the hand might guide the tracing pin of a polar planimeter. The eye is on average 10 to 15 cm away from the tracing point, so it can see it within a good visual distance and at the same time regulates the movement of the planimeter itself without any difficulty. In the end position sR1i1, the wheel r is locked in R1 by pressing it onto the axis acting escapement screw and frame a is turned until the thread f goes through the point R on the paper base p, which is in its initial position.
The problem can now be considered solved, because the ordinate of the index, which is now in i1, is the desired mean ordinate (height) of the curve k between U and U1. It can be read directly on the recording strip, which often has a graduation like meteorological thermograms, down to 0.05 graduation lines. If the thread is 20 cm long, you can measure curves 4 to 40 cm long at once. The layout of the paper p in Fig. 2 is particularly suitable for evaluating curves whose wave height is not large (e.g. less than 10 cm). For curves with a wave height of 15 to 30 cm, place the edge of the paper (Fig. 3) in the ordinate of the starting point U (Fig. 2) so that the extension of the perpendicular extends approximately through the easily estimated, sought-after point i1 (Fig. 2 u. 4), i.e. goes through the middle of curve k [The planimeter is initially positioned with the wheel in R (Fig. 2) at an angle to l, so that the optical travel begins again in U.] It can then never happen that F1 falls into the lateral sweep of l after tracing, the use of which may be necessary and permitted during optical tracing.
If the system p is unfavorable, the thread f in its final position RR1 (Fig. 2 and 4) deviates greatly (more than 10°) from its initial position FRAb and hits the fork in the curve shown on p. It is then necessary to advance the instrument further in its own direction RR1 by the small piece that the two branches of the curve cut off on the thread before reading from the index in i1. The change in the value of the average height amounts to a maximum of a few tenths of a millimeter. The displacement itself can be carried out either by eye or with the help of a pencil, etc., which serves as a sighting mark and is placed across the frame at the relevant point.
The planimeter only delivers theoretically correct results if the pen of the recording device moves, not on a circle, but on a straight line parallel to the ordinate axis. However, the resulting inaccuracy is not noticeable on the recording strips of meteorological devices of this type, since the arm carrying the pin is very long in relation to the wave height of the curves. In the case of strongly curved vapor voltage curves, this may need to be taken into account by applying a correction [4]. If you want to check the result by tracing from a different starting position, it is best to trace the curve in the opposite direction and average the results (see the last section).
In an adjusted optical planimeter, the axis of the wheel, which is perpendicular to the thread line, passes through the extended mirror plane, which is perpendicular to the base. If, under this assumption, FRU in Fig. 4 denotes the initial position of the planimeter on the base p, then U is the optical image of F and FU = 2FR = x0 = 2 ξ0.
If the optical tracing point U passes to U1 along the curve
k to be evaluated, then
![]()
Then, because F1 U1 touches the path q of the wheel,

or
from which follows through integration
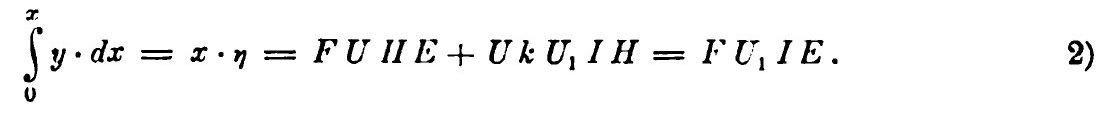
After rotation around R1,
F2RMR1I1 is the end position of the planimeter.
If M lies on the extension of y0, Fig. 4 shows that
![]()
As the parallelograms FUHE and F1MHE have the same area and
Eq. 2) with Eq. 3) are identical, it follows that
![]()
If L is the center of MI1, then the perpendicular must be
LL1, i.e. according to Eq. 3a) be the desired mean ordinate of the curve
piece k with respect to HI as the abscissa axis. Furthermore, after
constructing M and L, the equations exist
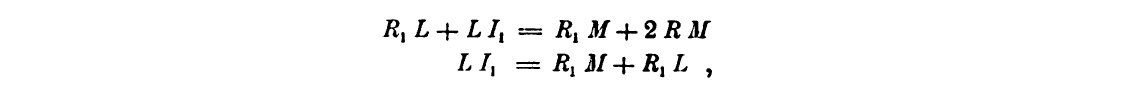
from which, by subtraction, R1L = RM [5]. If F2R is only slightly inclined (φ < 100) against the axis direction, then RM = RU, and L then coincides with the index of the instrument located in i1. Since R1i1 = RU, we have the formula for the small distance i1L by which the desired point L is still away from the index of the planimeter
Since RU is constant equal to 24mm, the displacement i1L depends only on the inclination of the thread RF2 (Fig. 4), so the curve (Fig. 3) can be constructed according to the following table:
Instead of making a shift in the direction F2R, you can also influence the same on the middle ordinate LL1
which is calculated in column 3, can be read off on a scale parallel to l.
From Eq. 2) follow the equations for the curve q (Fig. 4), the mean integral curve of k [6], which describes the wheel during optical travel, with the parameter x,
It is often desirable to draw this curve, which graphically represents the growth of the mean. This is done either with carbon paper, which is placed under the wheel, or, as can be seen from Fig. 1, by adding ink to the wheel in a drawing pen or sleeve, which consists of black, unwashable drawing ink, gum arabic, glycerine and water mixed in proportions 0.35: 0.25: 0.3: 0.1. The planimeter then automatically draws a deep black, evenly thick line on the paper, which dries quickly and lasts well. For example, if k is a straight line, then q becomes a hyperbola with the asymptotes l and k, which follows from Eq. 5).
The planimeter is therefore particularly suitable for precisely drawing hyperbolic and other isopleth tables, which are widely used in technology. If you want to draw a hyperbola, of which a point P and the lines l and k are given as asymptotes, you bring the locked wheel to P and turn the planimeter until the optical tracing point k hits. After releasing the escapement screw, k is driven optically while the wheel writes the hyperbola automatically.
Eq. 3a) shows that the apparatus can also be used as a linear planimeter, because the area below k (Fig. 4) is the product HI.LL1. The figures formed only by curves can also be calculated in a similar way. If one imagines the area from a point U divided into two approximately equal parts, place the system p (Fig. 3) in U in such a way that it does not cover the figure and determine the mean height point L' and L" for each part. Then the entire area is equal to L'L".HI.
The simplest, although not quite as accurate, method for calculating curvilinearly bounded areas follows from Eq. 1):
Because U is identical to U1 (Fig. 5) it follows
As the mirror can be used from both sides, the planimeter can also be turned over so that the frame falls over the figure k (Fig. 5). Using a slider with a mark, which is held in two grooves within the frame, you set RU = ½FU approximately equal to 10, choose the edge of a ruler at a distance of RF equal to 10 as a replacement for the line l and go around k optically, so that the image of the thread intersects the edge of the trace in F1. The area is ten times the difference in reading on the scale at F and F1.
With the rotor as a mark, the apparatus can be used effectively like a Prytz rod planimeter. Here, the wheel marks in the paper can be avoided if the mirror image of the thread is cut with a prismatic ruler.
An approximate perspective-optical area calculation of larger areas of several square meters with the small instrument can easily be carried out in the following way. Cover the paler side of the mirror facing away from the observer with paper except for a small, three millimeter wide opening S, place white cardboard on the edge of the table (Fig. 6) and draw the line l through F parallel to the edge. A larger piece of surface lying on the floor with the center in U is optically traced with the planimeter FRS standing on the table level using the small mirror opening S, after U is connected to the circumference of the figure by an arbitrary line. As in Fig. 5, let F1R1U1 be the end position.
If you set n = FR/NU, then this is the area of the piece lying on the ground:
The points FRNU are determined once and for all and a round number is chosen for FR/n2 so that areas can be read from l without calculation. It is advisable to repeat the route if you reverse the area and average the two results. The most accurate results are achieved with a metal mirror that has a small circular or oval opening. Planimeters, which are suitable for calculating such large areas, are commercially available under the name "leather measuring machines". Compared to this small instrument, all previously constructed mechanical devices for the direct measurement of leather and fur are characterized by their significant size and weight, without being any easier or more precise.
The correctness of the latter type of calculation can be proven using Figures 4 and 6. In Fig. 6 behaves
This ratio of x:ξ exists generally, so that for Eq. 1) is to be written
If one replaces x by ξ on the left, then partial integration follows
If the curve closes, then
and because the image of l at the initial point passed through the center of the figure k, approximately
As RR1 also roughly halves the remaining figure q, then
A contraction results in Eq. 6).
A number of screws allow the thread, wheels and mirror to be adjusted. You can check whether the mirror is perpendicular to the base according to what was said in the first section or by ensuring that two points that are the same distance (15 cm) from the wheel, e.g. F1 and U1 (Fig. 4), optically align.
When measuring recording strips, it is actually unnecessary to adjust the wheel because the error, if the index i falls within the extension of the thread, is proportional to the length of the abscissa and can therefore be correctively added to the result. If the wheel and thread form small angles with the mirror normals, and as a result the index i deviates to the right (left) by Δ0i (e.g. 0.90 mm) after optical travel for the abscissa x0 (e.g. 300 mm). (Error in the middle ordinate LL1), the correction for LL1 is at any abscissa x (e.g. 120 mm)
One determines Δ0i empirically as half the difference between the results of two optical measurements of a wave-shaped curve k with the abscissa length x0 when one traces the wave line in the opposite direction for the second time, i.e. the paper is reversed. In order to determine the accuracy of the measurement of registered curves in general with an optical planimeter, a large number of mean heights of 4 to 30 cm long thermograms were determined once by calculation by averaging and then by optical inspection and from the deviations an average error of the individual observation of only ± 0,07º C. (0.07 mm) was found. This error does not increase noticeably as the curve length increases. If observations are also made at regularly recurring intervals which must be taken into account when evaluating the results recorded by the recording device, the optically obtained result is subsequently improved by an averaged interval correction.
In contrast, precise adjustment is required to draw hyperbolas. After the wheel has been brought into the thread line, the axle is placed perpendicular to it and whether this has been achieved is checked by moving a thread point along a straight line without the wheel leaving it. Now place the mirror approximately vertically and place the bridge on the lower part so that the mirror plane points to the wheel axis, making sure at the same time that the mirror image of the thread falls into its extension. The mirror holder hits a screw that has to be adjusted so that the mirror is immediately in the correct position when opened. The Planimeter draws hyperbolas almost as precisely as a compass draws circles.
The instrument gives good results as a linear planimeter. The average error is only ±0,3% for medium-sized areas (1 qdm), and little more for small ones, while the calculation according to Fig. 5 is less precise and particularly dependent on the nature of the card paper. On a flat surface, the average error for small areas is ± 0,6%, but increases slightly with the size of the area.
The perspective calculations according to Fig. 6 suffer from a strong parallax of the optical tracing point and from estimation errors regarding the correct position of U, so that errors of 1 to 3% are to be expected. For this reason, the determination of the moments of small figures, which can be achieved by suitable integration of Eq. 7) is made possible, and enlarging and reducing figures is not mentioned.
Berlin, Agricultural University, January 1911.