

The instrument shown in Fig. l, called a compensation rod planimeter [1], is for the precise calculation of the area of curvilinear figures and for the evaluation of registered curves. It resembles in shape the Prytz rod planimeter [2], which has been known since 1886; an invention that has often been discussed in specialist journals. This communication is intended to give a description and theory of this new planimeter, and also to consider its advantages and disadvantages in comparison with other systems, paying particular attention to their accuracy.
This rod planimeter differs significantly from the Prytz instrument in that for it to move around a figure with the tracing pin, the rod a is placed over the edge of a roller r (Fig. l upper and lower) or on a ball (middle instrument). As it rolls, the distance between the rollers and the tracing pin does not remain constant (as with Prytz), but changes continuously. At the end of the rod is a reading device with an index line e and the rod rests on the paper at three points: on the tracing pin, the wing handle and the edge of the roller. The roller is cylindrical, with a protruding sharp edge which is held in a groove s in the rod, while the cylinder presses it laterally against the groove, so that it only rolls in the direction of the rod and the planimeter cannot fall over.
For area calculation, e.g. plot 8 (Fig. 1), place the tracing pin on any point on the contour so that the rod does not cover the area and is directed approximately towards its center, while the right edge of the roller rests at one of the marks on the groove s. Align the rule [3] eb with the scale c against the instrument so that the zero division is approximately perpendicular to the index line i of the rod. The scale rule has a needle point at b (similar to the pole of a polar planimeter)) which rests on the paper, and you can rotate the scale around b to push it to the side while tracing the surface. After a clockwise circuit, bring the scale back to the index line i of the rod by turning at b, and take a new reading. Ten times the reading is the simple or double the area of the figure measured, depending on whether the roller was set to the left or right mark on the rod.
However, at least for larger areas and precise calculations, this value still requires a small correction, which depends mainly on Φ itself, but also on a ratio v. v is estimated from the position of the rod in relation to the figure and is the ratio of the diameter of the area in the direction of the rod to the diameter in the direction perpendicular to the rod. v is equal to one for all approximately round or square figures. For the multiplication constant 10 (roller distance from the pen 20 cm) the following correction table applies, which is only partially reproduced here. The arguments are the area Φ and the v to be estimated in 1:1000, the corrections mean square meters.
The ratios v are listed in column 1 from 4 to 1/3. It is well known that with the polar planimeter there are certain favorable configurations that can be expected to produce particularly precise results, and that is also the case here. Table 1 provides information about this important question and makes it clear that with larger, highly irregular or very elongated figures one can expect a more precise result if the rod is placed in the direction of the largest diameter of the surface, i.e. if v>1, because an error in estimating v then only means a very small error in the correction. As an example of the calculation process and the use of Table 1, a calculation of plot 8 in Fig. l is used, the area of which on the scale l:1000 has the target value of 4347 sqm if v was estimated at 1/2:
Ten times reading: 4325
Correction: 10
Area: 4335
A significant error in v would change the result by at most 5 to 8 square meters or ± 0.2 percent. The roller regularly returns to the mark for small figures, but occasionally not exactly to the mark for larger figures. This deviation Δ is estimated in mm in order to use it and the area Φ to derive a correction from the following table: [For the 24 calculations on the map in Fig. 1, Table 2 was used only once.]

Here the value A in millimeters is regarded as negative if the roller is closer to the tracing pin after a circuit and vice versa. Strictly speaking, even with a large P, it becomes zero when the bisecting line of the angle that the initial position makes with the final position of the rod passes through the center of gravity of the figure. Therefore, when calculating large areas (larger than the size of your hand), you can first make a superficial test tracing to see whether Δ almost disappears. Such an experiment would correspond to a similar test to be carried out with the polar planimeter to see whether the area can be calculated. On the other hand, a look at Table 2 shows that this correction for negative d is small (only about 0.1 percent of the area) and can be neglected. This is based on the simple rule of placing the rod in such a way that its extension either halves a larger figure, or that the part of the area facing the computer becomes the larger, up to 2/3 of the entire area.
An advantage over the polar planimeter is the quick change of the multiplication constant 5 or 10 without having to loosen screws. Figures up to 30 cm long can be measured. If they are larger than about 2 sq. cm, or so irregular that they cannot be roughly estimated, they must be measured separately in two parts. If a second compensating tracing is to be made, choose a position of the rod that is approximately perpendicular to the first in order to eliminate any inaccuracies resulting from an incorrect estimate of v. With the polar planimeter, a repeat measurement is often made in order to make the reading errors as harmless as possible by moving around small figures twice in a row with a fixed pole position, but this achieves little advantage because the roller makes the same path each time. This latter is not the case with the rod planimeter, so the advantage is fully exploited.
For calculations on poor paper, or if there is no space for the roller on the map because the figure is on the edge, run the roller on a 5 x 10 cm zinc plate included with the planimeter. It is also sufficient for large areas up to 20 cm long because the roller only covers half the travel of the tracing pin compared to the polar planimeter. Imperfections which have an unfavorable influence on the guidance of the tracing pin cannot occur with the planimeter rod, as they occur with various planimeters, but especially with the Lippincott planimeter from the inclined position from the tracing arm to the pole arm. With a tapered map scale, e.g. 1:2000, the reading difference d must be on the prismatic scale instead of 5 or 10 with 20 respectively be multiplied by 40. But if the constants are no longer round numbers, you choose other marks on the rod or a suitable measuring scale.
Experiments show that strong bending of the rod has no effect on performance and accuracy, so that it can be safely handed over to untrained people.
The precision investigations that follow are based on calculations of the map shown in Fig. l which has 24 different sized, very irregular figures and an area of almost 12 hectares at 1:1000. To calculate the target values, the average (column 2 of the following table) was formed from three circuits with the free-floating precision spherical planimeter Coradi No. 612 (price 150 M.), a collection item in the Geodetic Department of the Agricultural University, set to the constant l. Each figure was then traced once (very small figures twice) with the Coradi compensation planimeter No. 2002 (price 65 M.), whose roller skew has been eliminated. The summation of the results resulted in a deviation of -225 per 119,605 square meters, which was distributed proportionally. The difference between the reduced values and the target in column 2 is shown in the third column of the table. In order to be able to compare the accuracy of the rod planimeter with that of the chosen compensating planimeter (Fig. 2, below), each figure was measured just once with rod no. 13, with the roller set to the multiplication constant 10, or for very small figures 5, and the deviation from the target (column 2) entered in column 4 each time. Two further calculations carried out under the same conditions with bars no. 13 and 14 revealed the errors in the last two columns. Plot 20 was always divided into two parts due to its shape. The area summation showed errors of -63 respectively for the first two calculations. 6 square meters against 119605 square meters. In the third calculation made a few weeks later, the card had fallen by 0.1 percent, while the final deviation was -127 square meters. Here the rod was intentionally placed unfavorably, i.e. with v < l.
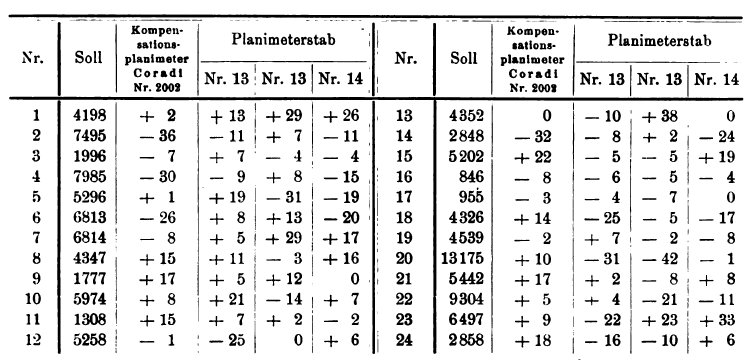
Each of the calculations in columns 3 to 6 took almost two hours, so each result took about 4 minutes. If μ denotes the average error of a single area calculation in square meters on a scale of 1:1000 and Φ denotes the area in square meters, the above compilation results in the following formula both for Coradi's compensation planimeter (column 3) and the new rod planimeter (columns 4 to 6).
The formula generally expresses that both instruments can be regarded as equivalent in terms of their accuracy. The accuracy of the expensive precision planimeters, which cost around 150 M., is considerably greater, of the order
The results of the above calculations are shown graphically in Fig 2. The area Φ in square cm is entered as the abscissa and its calculated mean percentage error as the ordinate. Curve 1 parallel to the axis represents approximately the error of a Prytz rod planimeter after a circuit made from the estimated center of gravity, curve 2 represents the average error of the Coradi No. 2002 compensating planimeter in percent of the area, curve 3 (the solid line) that of the new rod planimeter and curve 4 that of the free-floating precision spherical planimeter of Coradi, as it resulted from the calculation in column 2 for a single tracing.
Theory of the compensation rod planimeter and the determination of the mean ordinate of registered curves.
The way it was created, the compensation rod planimeter can be viewed as a simplification of the "optical planimeter" [4]. In Fig. 3, let R be the roller and U the tracing pin of the rod at the starting point of the curve UU1 to be evaluated. If you imagine the reflective plane of the optical planimeter above the roller perpendicular to the rod and to the paper, then U is the optical tracing point and image point of the intersection of a line l with the direction RU (the thread line).
With the rod planimeter, the rod touches the roller (ball) in R, so that the rod moves in its own direction as quickly as the roller and the roller must always be in the middle between the fixed point F and the tracing pin. When the rod rotates, the geometric location of F in the differential sense is a piece of a circle, whereas with the optical planimeter this curve can be chosen arbitrarily.
However, the formulas developed in [4] cannot be easily applied to the rod planimeter because, firstly, the line l was assumed to be a straight line and secondly, at least when using a sphere, RF is slightly larger than RU. In this case, the rod touches the ball, which sinks slightly into the groove, at two points, so that a general statement can be made.
The actually circle-like curve l from the equation z = f(t) is arbitrarily distorted in Fig. 3 in order to give a clear, geometric explanation of the following theory. As the involute of the roller path q, whose coordinates are N and F, it has return points, the number of which depends on the shape of the curve to be evaluated y = f(x). According to Fig. 3
If you replace dξ on the left; according to Eq. 1), then
The figure now results in η-z = n(y-η). If one inserts y or ξ from this equation and from Eq. 1) into the last two terms of Eq. 2) one, it follows
or by decomposition
If you replace dx - dξ according to Equation 1) and integrate, you will find the area formula
This formula can be explained geometrically as follows for n=1 (sharp-edged roller):
This proves that
If one takes into account that the line l can in reality be viewed almost as a circle with a fixed radius, one only has to connect the points R and R1 marked by pressing on the rod [5], this line around RU beyond R1 to L to extend and can pick up the middle ordinate LL1. However, in order to obtain accurate results, the rules applicable to the initial position of RU for the optical planimeter must be observed (see also [4] page 67).
If, on the other hand, UU1 is a closed figure with the content Φ (Fig. 4), i.e. U is identical to U1, I is identical to H, then the so-called residual figure becomes for n = 1
and Eq. 4) becomes
or Φ = sector UFF1. If RU and R1U are symmetrical to the line of gravity, including q and l, then RU = R1U or Δ = 0. With constant RU, the area Φ is proportional to the angle FUF1, apart from a correction regarding the shape of the area.
Table 1 was calculated by graphically integrating differently shaped figures and with changing v with the aid of interpolation, so that it also includes the system of the scale eb (1: m.1000) shown in Fig. 1 and the reduction of the straight line ii1, which the circular sector FUF1 is taken into account. If p is the distance of a mark from the tracing pin, r is the radius of the roller (ball), k is the multiplication constant 5, 10, etc. and w is the length of the rod iU, then the formula applies to p.
A theoretical series development [6] for the correction table 1 has been omitted at this point. If the ball sinks halfway into the bar frame, then n = ∞ and the rod planimeter becomes a Prytzian bar planimeter, whose performance greatly affects the remaining figure q. In the case of the ball bar shown in Fig. 1, however, n = 1.05 and the influence of q is harmless.
Although the accuracy of the most expensive precision planimeters costing over 100 M. cannot be achieved with this new planimeter, it has been shown that the rod planimeter produces results that are just as accurate as the compensating polar planimeter that is available on the market but is twice as expensive.
Berlin, Royal Agricultural University, March 1911.